Computational thinking can be defined in many different ways. Some attach the use of computers and computer programming to the definition. While it is important to note, especially in our technology-filled world that computational thinking and computers are intrinsically linked, there is a simple unplugged definition. Computational thinking is the process of solving problems by breaking them down into steps (Victoria, 2018). Often, the steps are written into a pattern or algorithm that then becomes computer code. However, there are many ways to teach computational thinking skills in an unplugged, or nearly unplugged fashion.

Math anxiety, the fear of math. It is real. Many adults and so many students struggle with math anxiety. As a career and technical education (CTE) teacher, I am in a unique position to approach “math instruction” from a low stakes angle with students. In fact, often when students are creating their quilts, they do not even realize that they are doing complex math skills.
The question I wanted to explore for module 3 was: How might atypical, surprising, and unplugged computational thinking exercises be an inclusive way to engage all of my students in this type of problem solving? This fits in with the International Society for Technology in Education (ISTE) standard 1.5 – Computational Thinker. Specifically, standards 1.5c – “Students break problems into component parts, extract key information, and develop descriptive models to understand complex systems or facilitate problem solving,” and 1.5d – “students understand how automation works and use algorithmic thinking to develop a sequence of steps to create and test automated solutions” (ISTE, n.d.).
According to the University of Canterbury, New Zealand, unplugged lessons in computational thinking can be broken down into 5 simple steps. These steps are: describe a problem, identify important details needed to solve, break the problem down into smaller steps, use the steps to create a process (algorithm) that “solves” the problems and then evaluate the process (CS Unplugged, n.d.). What I like about these steps is that they directly relate to designing a quilt:
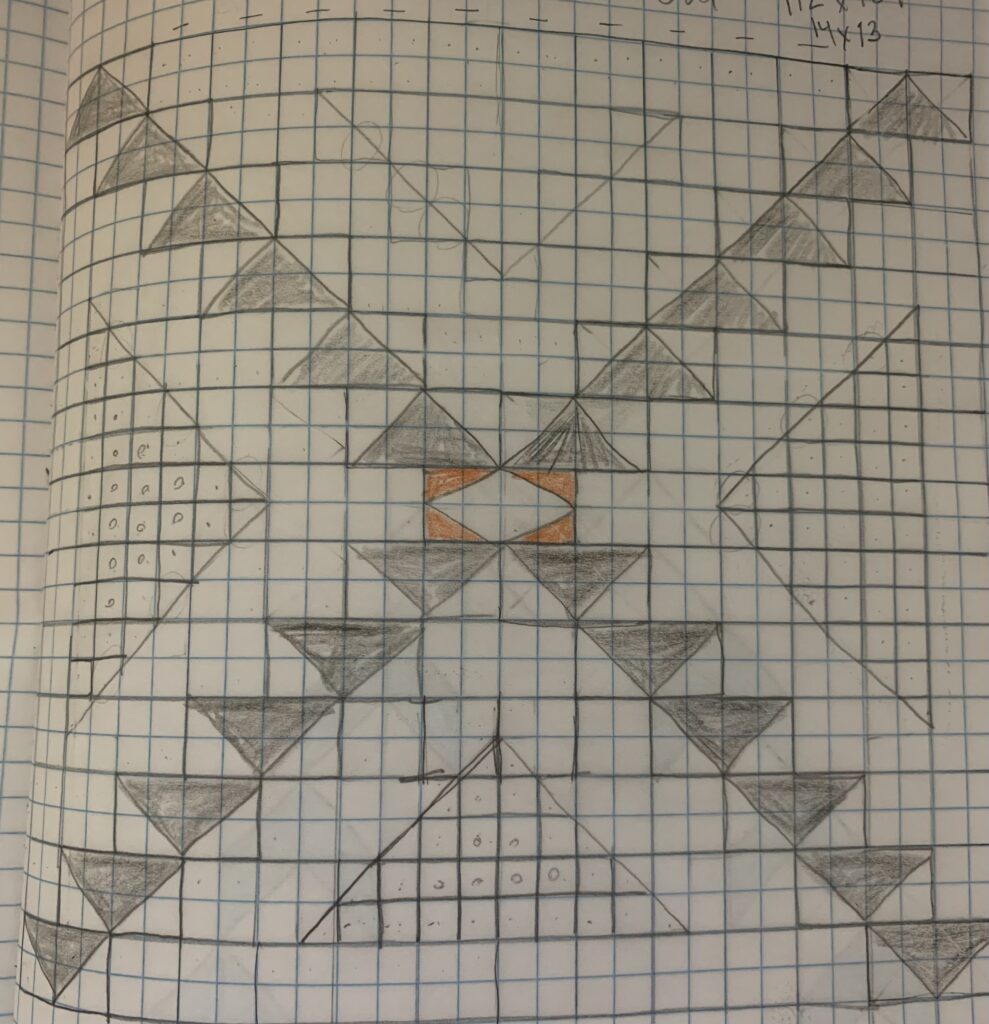
Step 1: describe a problem. In the case of quilting – draw a design you would like to make. Oftentimes students will draw blocks or shapes they are already familiar with, using graph paper.
Step 2: identify important details. How many different colors do you need, what types of shapes are in the pattern, etc.?
Step 3: break the problem into smaller steps. Using the formula that 1 square equals 1 inch, students begin to count the squares and figure out how many of each shape and size they will need.
Step 4: write the algorithm. Once all information has been gathered, students begin to write a pattern (algorithm) for how to physically create the block/quilt.
Step 5: evaluate the process. After writing down the steps in the pattern, evaluate the process by following the pattern, step by step to see if the pattern can be recreated using fabric or construction paper. As with any design process, if the pattern/algorithm cannot be accurately replicated, then return to step 4 and work out the kinks.
I am not the first teacher to think of using quilts to teach computational thinking skills. In fact, I have found articles from thirty years ago of teachers using quilting to teach multiple mathematical concepts. According to Paznokas, quilts can be used to teach about culture and multiple mathematical concepts including: symmetry, ratios, economics – cost of making a quilt, tessellations, fractions, and geometry (2003). Many teachers begin teaching quilting by using tangrams and tessellations. Code.org has many computer science fundamentals lessons available in an unplugged format. My favorite is tessellations and tangrams. The reason I like tangrams for teaching quilting and computational thinking is because the student is given a group of shapes and asked to arrange those shapes into larger more complex shapes, this is the basis for all quilt designs. Students are designing a quilt without realizing they are.
During my research I came across a, revolutionary to me, math program at the University of Wisconsin-Eau Claire. Dr. Simei Tong took a freshman level math class and turned it on it’s head. The class was titled “Introduction to Mathematical Thinking” and the students created quilts from the design phase, all the way to the completed product, while learning geometry along the way (Berthiaume, 2017). The course received high praise from students, with one student stating that it was the first math class they ever liked.
One thing that is important to emphasize is that quilting and quilt design do not need to be done solely with pencil and graph paper. There are multiple quilting programs available for purchase in order to design quilts and quilt blocks. Many of these programs are quite expensive and therefore may not be cost effective for the classroom. However, There are also some ways to design quilts digitally with free computer applications. For instance this quilt was designed entirely in Google Slides for free:

This quilt design covers multiple mathematical concepts including: translation, rotation and reflection. By changing the size of the blocks dilation is also involved.
Having students participate in the quilt design process; taking ownership of each step is a wonderful, though clearly not novel, way of incorporating quilting into math instruction. For my purposes, I am working backwards. I am using my quilting class to teach math concepts in an inclusive way that allows students to see the artistry involved in math. In this manner, students are learning and demonstrating computational thinking skills without ever having to step foot into math class. When anxiety is involved, in any subject, guiding students towards the beauty and artistry of the subject can go a long way to ease fears. Computational thinking through quilting has the ability to do this.
References (cited and additional):
Alegre, F., Underwood, J., Moreno, J., & Alegre, M. (2020, March 11-14). Introduction to computational thinking: A new high school curriculum using CodeWorld [paper presentation]. Special Interest Group Computer Science Education, Portland, OR, United States. https://doi.org/10.1145/3328778.3366960
Anthony, H., & Hackenberg, A. (2005). Making quilts without sewing: Investigating planar symmetries in southern quilts. Mathematics Teacher, 99(4) 270-275.
Berthiaume, J. (2017, December 13). Bringing math concepts to life through quilting. University of Wisconsin-Eau Claire. https://www.uwec.edu/news/news/bring-math-concepts-to-life-through-quilting-2735/
Bohning, G., & Williams, R. (1996). Quilts and tangrams: Linking literature and geometry. Childhood Education, 73(2), 83-87. https://eric.ed.gov/?id=EJ536378
Hede, J. T., & Bostic, J. D. (2014). Connecting the threads of area and perimeter. Teaching Children Mathematics, 20(7), 418-425.
Kolodner, J. L., & Lamberty, K. K. (2002). Exploring digital quilt design using manipulates as a math learning tool.
Mann, E. (2009). The search for mathematical creativity: Identifying creative potential in middle school students. Creativity Research Journal, 21(4), 338-348. https://www.tandfonline.com/doi/abs/10.1080/10400410903297402
Paznokas, L. (2003). Teaching mathematics through cultural quilting. Teaching Children Mathematics, 9(5), 250-256.
Roscoe, M. B., & Zephyrs, J. (2016). Quilt block symmetries. Mathematics Teaching in the Middle School, 22(1), 18-27.
University of Wisconsin-Eau Claire. (2017, December 13). Stitching with Strategy: Math Quilts [Video]. YouTube. https://www.youtube.com/watch?v=_JJJfss2woI
Victoria, Katie (2018, December 29). What is computational thinking? Why thinking like a computer builds skills for success.Teach Your Kids to Code. https://teachyourkidscode.com/what-is-computational-thinking/Wickstrom, M. (2014). Piecing it together. Teaching Children Mathematics, 21(4) 220-227.

7 replies on “Quilt Math – Computational Thinking in Action”
I feel touched with this statement, “When anxiety is involved, in any subject, guiding students towards the beauty and artistry of the subject can go a long way to ease fears.” Thanks for sharing this insightful teaching practice!
Thank you Ignasia. I grew up as someone filled with math anxiety and it took becoming a published pattern designer to help me realize I was actually good at math, I just needed to figure out a way to make it relevant to my own life.
Melissa,
I am intrigued by your post. You beautifully take the two subjects and make combine them in such a practical way. While I love math, quilting to me was overwhelming. If a student were overwhelmed with one of them, after reading this can use skills in the one they are good at to master the other. I also love your examples and thought it was brilliant how you used Google Slides for making one. Where can I sign up?
I get asked that question a lot. Quilting can be overwhelming for my students at first. I always ease into it with the basics, once they have a victory or two under their belts, I’m only in the room because an adult is legally required. The kids just do such a good job!
Thanks, Melissa. You have broken down the steps of computational thinking in a very clear and succinct way. I love this statement, “students are learning and demonstrating computational thinking skills without ever having to step foot into math class.” I do remember when I made my first quilt 2 years ago when my son graduated from high school. It was a lot of work and I could see how computational thinking helped me break down the daunting task into smaller, more manageable bits. Thanks for your post!
Thank you Chelly. It took me years to finally regard myself as good at math, and it is all thanks to quilting. I was one of the math anxiety kids and quilting helped me conquer that. Seeing the practical application of a skill is sometimes all we need to get over the fear.
[…] have written before about the math heavy nature of quilting, see my post on computational thinking and quilting. The idea I came up with was to find a class in another school that was working on a geometry unit. […]